

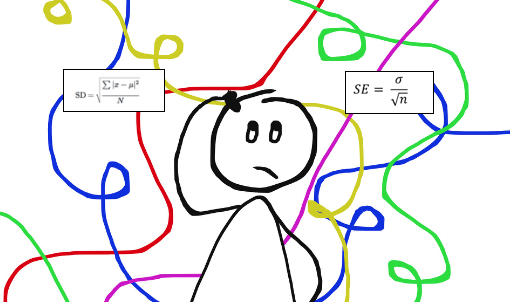
The equation is essentially the same excepting the N-1 term in the corrected sample deviation equation, and the use of sample values.
#How to calculate standard error of estimate how to#
Refer to the "Population Standard Deviation" section for an example of how to work with summations. As such, the "corrected sample standard deviation" is the most commonly used estimator for population standard deviation, and is generally referred to as simply the "sample standard deviation." It is a much better estimate than its uncorrected version, but still has a significant bias for small sample sizes (N<10). Unbiased estimation of standard deviation, however, is highly involved and varies depending on the distribution. The equation provided below is the "corrected sample standard deviation." It is a corrected version of the equation obtained from modifying the population standard deviation equation by using the sample size as the size of the population, which removes some of the bias in the equation. It is worth noting that there exist many different equations for calculating sample standard deviation since, unlike sample mean, sample standard deviation does not have any single estimator that is unbiased, efficient, and has a maximum likelihood. A common estimator for σ is the sample standard deviation, typically denoted by s. In many cases, it is not possible to sample every member within a population, requiring that the above equation be modified so that the standard deviation can be measured through a random sample of the population being studied. Hence the summation notation simply means to perform the operation of (x i - μ 2) on each value through N, which in this case is 5 since there are 5 values in this data set. for the data set 1, 3, 4, 7, 8, i=1 would be 1, i=2 would be 3, and so on. The i=1 in the summation indicates the starting index, i.e. In cases where every member of a population can be sampled, the following equation can be used to find the standard deviation of the entire population:įor those unfamiliar with summation notation, the equation above may seem daunting, but when addressed through its individual components, this summation is not particularly complicated.
The population standard deviation, the standard definition of σ, is used when an entire population can be measured, and is the square root of the variance of a given data set. The calculator above computes population standard deviation and sample standard deviation, as well as confidence interval approximations. When used in this manner, standard deviation is often called the standard error of the mean, or standard error of the estimate with regard to a mean. In addition to expressing population variability, the standard deviation is also often used to measure statistical results such as the margin of error. Similar to other mathematical and statistical concepts, there are many different situations in which standard deviation can be used, and thus many different equations. Conversely, a higher standard deviation indicates a wider range of values. The lower the standard deviation, the closer the data points tend to be to the mean (or expected value), μ. Standard deviation in statistics, typically denoted by σ, is a measure of variation or dispersion (refers to a distribution's extent of stretching or squeezing) between values in a set of data. Related Probability Calculator | Sample Size Calculator | Statistics Calculator


 0 kommentar(er)
0 kommentar(er)
